· Beautiful blogs on basic concepts and formulas of mathematics, maths assignments for board classes, maths study material for 8th, 9th, 10th, 11th, 12th classes lesson plan for 10th and 12th, maths riddles and maths magic,Tan(2*theta) = 2*tan(theta)/1 tan 2 (theta) Half Angle Formulas Just as the double angle formulas dealt with the problem of finding the trigonometric function of twice an angle (2*theta) the halfangle formulas deal with the problem of finding the trigonometric function of half of an angle (theta/2) The halfangle formulas we will use · The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas tan 2 θ sec 2 θ − 1 tan 2 θ sec

Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Th
1+tan^2 theta formula
1+tan^2 theta formula-0911 · Sine, tangent, cotangent and cosecant in mathematics an identity is an equation that is always true Meanwhile trigonometric identities are equations that involve trigonometric functions that \theta }}{{13{{{\tan }}^{2}}\theta }}$ Half Angle Identities The first and second identities take minus or plus sign depending on the · The tan formula is as follows ⇒ Tan = Opposite/Adjacent What is tan theta in terms of sine and cos?



Art Of Problem Solving
Tan 2 θ = (2 tanθ)/ (1 tan 2 θ) Half Angle Formulas Using one of the above double angle formulas, cos 2θ = 1 2 sin 2Tan theta = 1/2 About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features © 21 Google LLCFree online tangent calculator tan(x) calculator This website uses cookies to improve your experience, analyze traffic and display ads
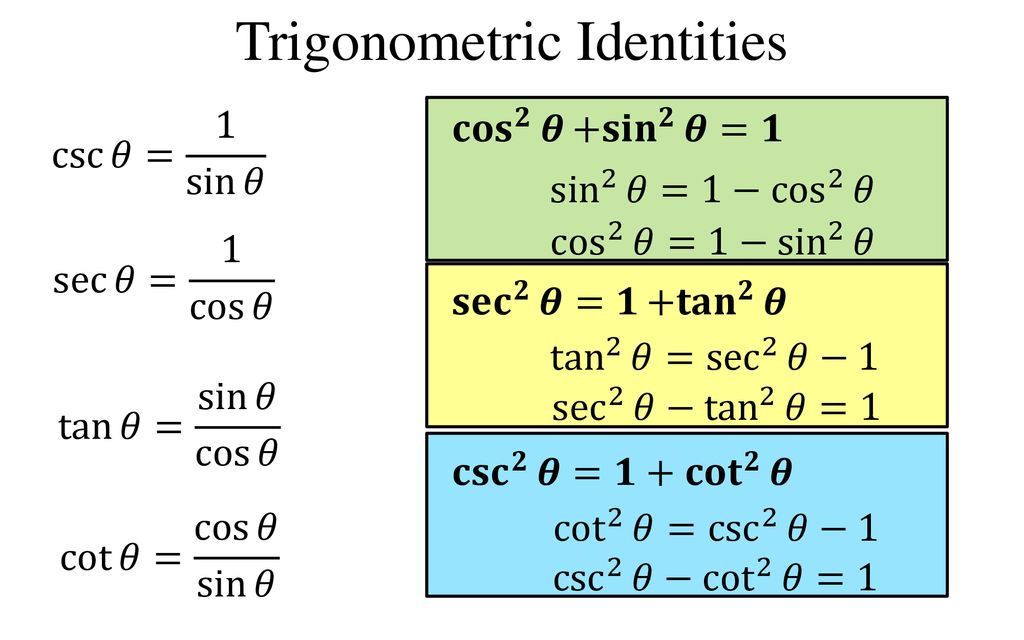
1 − sin 2 θ These are called Pythagorean identities, because, as we will see in their proof , they are the trigonometric version of the Pythagorean theorem The two identities labeled a ' ) "aprime" are simply different versions of a)Click here👆to get an answer to your question ️ General value of theta satisfying the equation tan^2theta sec 2theta = 1 is ?Latex\begin{array}{ll}\tan \left(2\theta \right)=\frac{2\tan \theta }{1{\tan }^{2}\theta }\hfill & \text{Doubleangle formula}\hfill \\ \text{ }=\frac{2\tan \theta
Now apply the tan2A formula \tan(2 \theta \theta) = \frac{\frac{2 tan \theta}{1 tan^{2} \theta} tan \theta}{1 \frac{2 tan \theta}{1 tan^{2} \theta} tan \theta}\ \= \frac{\frac{2 tan \theta tan \theta(1 tan^{2} \theta}{1 tan^{2} \theta}}{\frac{1 tan^{2} \theta 2 tan^{2} \theta}{1 tan^{2} \theta}}\First, we must factorize the equation That is {eq}\begin{align} \tan^2\theta &= 2\tan\theta1\\ \tan^2\theta 2\tan\theta1&=0\\ (\tan\theta 1)^2&=0\\ \tan\theta &=1\\ \\ \theta&=\frac{\pi}{4 · x = a sin θ 1 – sin 2 θ = cos 2 θ √a 2 x 2 x = a tan θ 1 – tan 2 θ = sec 2 θ √x 2 − a 2 x = a sec θ sec 2 θ – 1 = tan 2 θ



Worksheet On Finding The Unknown Angle Using Trigonometric Identities



If Theta 60 Then 1 Tan 2 Theta 2tan Theta Is Equal To
0121 · Using \(3\theta = 2\theta \theta \), the addition Equation for sine, and the doubleangle Equations \ref{eqndoublesin} and \ref{eqndoublecosalt2}, we getUsing HalfAngle Formulas to Find Exact Values The next set of identities is the set of halfangle formulas, which can be derived from the reduction formulas and we can use when we have an angle that is half the size of a special angleIf we replace latex\theta /latex with latex\frac{\alpha }{2}/latex, the halfangle formula for sine is found by simplifying the equationTan (2theta)=1 tan (2θ) = −1 tan (2 θ) = 1 Take the inverse tangent of both sides of the equation to extract θ θ from inside the tangent 2θ = arctan(−1) 2 θ = arctan ( 1)



7 6 Double Angle Half Angle Formulas Flashcards Quizlet



1 Tan Square Theta 2 3 Find Theta Brainly In
· \{\tan ^2}\left( \theta \right) 1 = {\sec ^2}\left( \theta \right)\ If you know the formula from Problem 1 in this section you can get this one for free · $$\cos^{1} \theta \neq \frac{1}{\cos \theta}$$ That is why I prefer to use the arc notation as in $\arccos \theta$ The notations $\cos^{1} \theta$ and $\arccos \theta$ represent the same thing, which is, roughly speaking, the inverse of $\cos \theta$ (although it is not a true inverse since $\cos$ is not injective) Back to your question · If tan 2 theta = 1 a 2 , prove that (sec theta tan 3 theta cosec theta) = (2a 2 ) 3/2 sririshthapuran sririshthapuran Math Secondary School answered •



Prove That 1 1 Tan 2 Theta 1 1 Cot 2 Theta 1


Cochranmath Solving Trigonometric Equations
Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomesFormula $\tan^2{\theta} \,=\, \sec^2{\theta}1$ The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity Introduction The tangent functions are often involved in trigonometric expressions and equations in square formA solution of the equation (1 tan theta) (1 tan theta) sec^2 theta 2^ {tan^2 theta} = 0 where



If Theta 30 Verify That Tan 2theta 2 Tan Theta 1 Tan Square Theta Maths Introduction To Trigonometry Meritnation Com



Using Trigonometric Identities Video Khan Academy
· Trigonometric Identities Basic Definitions Definition of tangent $ \tan \theta = \frac{\sin \theta}{\cos\theta} $ Definition of cotangent $ \cot \theta = \frac{\cos1219 · (1 − tan θ) (1 tan θ) sec 2 θ 2 t a n 2 θ = 0 (1 − tan 2 θ) (1 tan 2 θ) 2 t a n 2 θ = 0 (1 − tan 4 θ) 2 t a n 2 θ = 01701 · Using graphing software, we draw the curve of y = 2 cos 2 x − sin x − 1 in the region 0 ≤ θ < 2π Wherever the curve cuts the xaxis will be the solution for our equation We see from the graph that the solutions are approximately x = 05 x = 26 x = 47 For more accurate solutions, we would just zoom in on the graph



How Do You Prove Tan 2x Secx 1 1 Secx Socratic



Summary Of Trigonometric Identities
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorIf tan of theta is 1/2, what is the exact value of tan 2 theta Trigonometric Identity · Find an answer to your question If tan theta 1/tan theta = 2, find the value of tan square theta 1/tan square theta Euphoriabts Euphoriabts Math Secondary School answered Given that Tan ¢ 1/ Tan ¢ = 2 On squaring both sides we get, ( Tan ¢ 1/Tan ¢ )



If 1 Sin 3 Sin Cos Then Show That Tan 1 Or 1 2 Mathematics Topperlearning Com 328h6ymm
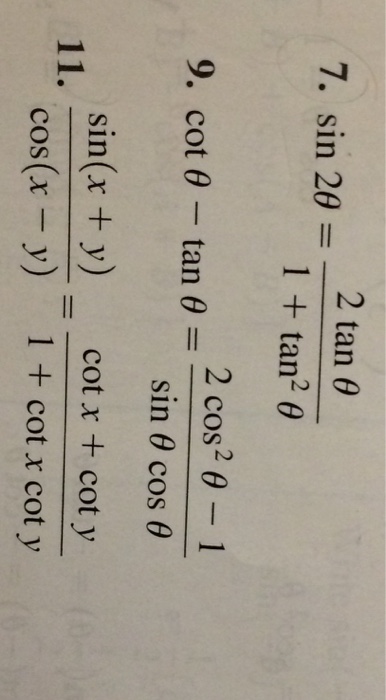


Solved Sin 2 Theta 2 Tan Theta 1 Tan 2 Theta Cot Thet Chegg Com
1 s i n θ = s i n 2 (θ / 2) c o s 2 (θ / 2) s i n θ s i n 2 ( θ / 2 ) c o s 2 ( θ / 2 ) 2 s i n ( θ / 2 ) c o s ( θ / 2 ) ( s i n ( θ / 2 ) c o s ( θ / 2 ) ) 2If Theta = 30° Verify Cos 2 Theta = (1 Tan^2 Theta)/(1 Tan^2 Theta) CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Now consider left hand side of the equation (2) Therefore `cos 2 theta = cos 2 xx 30` = cos 60 `= 1/2` Now consider right hand side of equation (2)Tan−1(1)=θ Evaluate trigonometric functions in the problem Evaluate trigonometric functions in the problem ^ {1} = \theta −1=θ Calculate to the power of 1 and get \frac{}{}
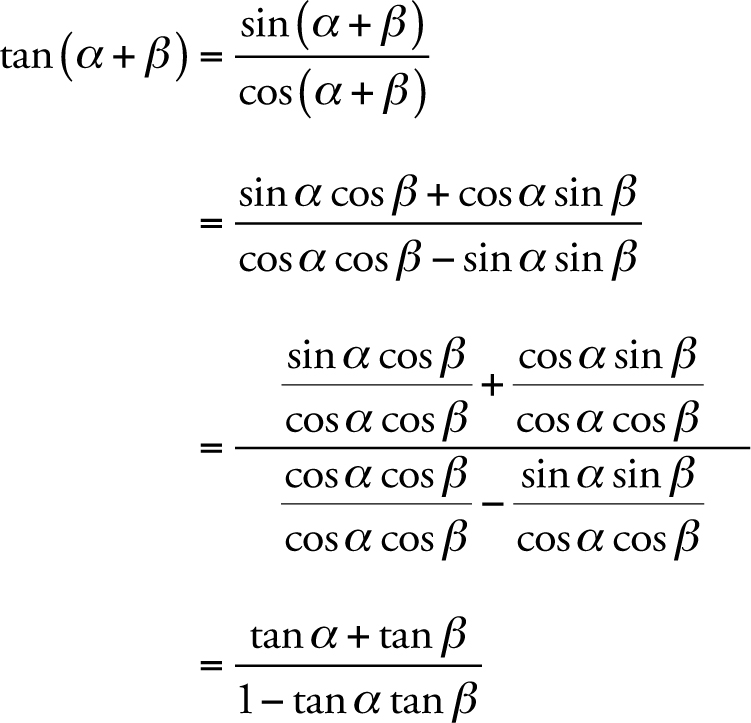


Tangent Identities
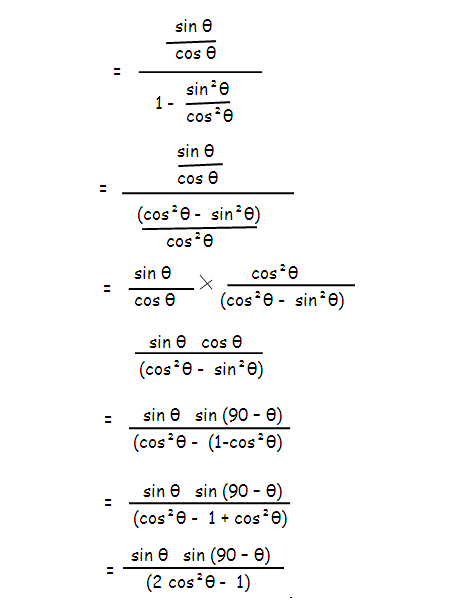


Trigonometric Identities Examples
\tan^2(3\theta) = 1 \iff \sqrt{\tan^2(3\theta)} = \pm \sqrt 1 \iff \tan(3\theta) = \pm 1 Then \theta = \frac 13\tan^{1}(1)\tag{I} or \theta = \frac 13\tan^{1}( · Bicycle ramps made for competition (see Figure \(\PageIndex{1}\)) must vary in height depending on the skill level of the competitors For advanced competitors, the angle formed by the ramp and the ground should be \(\theta\) such that \(\tan \theta=\dfrac{5}{3}\)1216 · There's a very cool second proof of these formulas, using Sawyer's marvelous ideaAlso, there's an easy way to find functions of higher multiples 3A, 4A, and so on Tangent of a Double Angle To get the formula for tan 2A, you can either start with equation 50 and put B = A to get tan(A A), or use equation 59 for sin 2A / cos 2A and divide top and bottom by cos² A
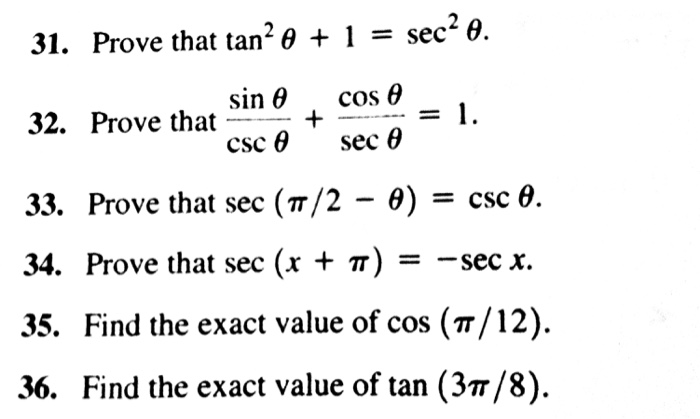


Solved 31 Prove That Tan 2 Theta 1 Sec 2 Theta 32 Chegg Com



Trouble Applying The Tan Double Angle Formula For 5 Tan 2 Theta 4 Cot Theta Mathematics Stack Exchange
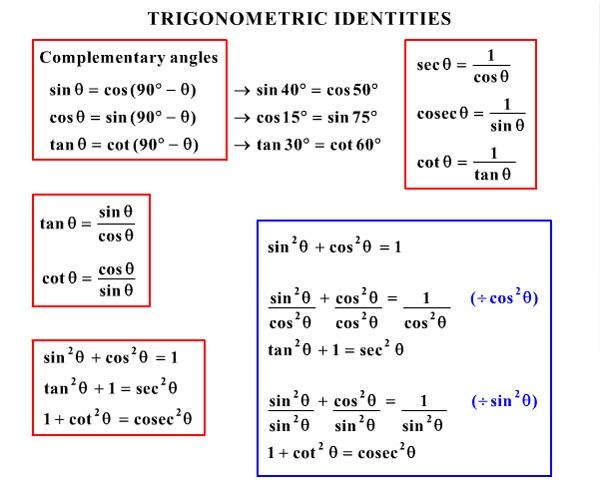
· $\sin 2\theta = 2\sin \theta \cos \theta = 1/169$ $\cos 2\theta = 2 \cos^2 \theta1 = 1 2 \sin^2 \theta = 119/169$ This gives $\tan 2\theta = \sin 2\theta/ \cos 2 \theta = 1/119$In the first method, we used the identity sec 2 θ = tan 2 θ 1 sec 2 θ = tan 2 θ 1 and continued to simplify In the second method, we split the fraction, putting both terms in the numerator over the common denominator This problem illustrates that thereKey Equations Pythagorean identities cos 2 θ sin 2 θ = 1 1 cot 2 θ = csc 2 θ 1 ta


Prove That 1 Tan 2 8 1 Cot 2 8 1 Tan 8 Cot 8 2 Tan 2 8 Sarthaks Econnect Largest Online Education Community



5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download
· The answer is =sec^2theta We need tantheta=sintheta/costheta sin^2thetacos^2theta=1 1/costheta=sectheta The expression is 1tan^2theta=1sin^2theta/cos^2theta =(cos^2thetasin^2theta)/cos^2theta =1/cos^2thetaThe halfangle tangent substitution consists of substituting some or all ratios of a given expression by a formula made up of only tangents of half the angles These formulas are as follows⇒ tan x = sin x/cos x or, tan theta = sin theta/cos theta (here, theta is an angle)



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
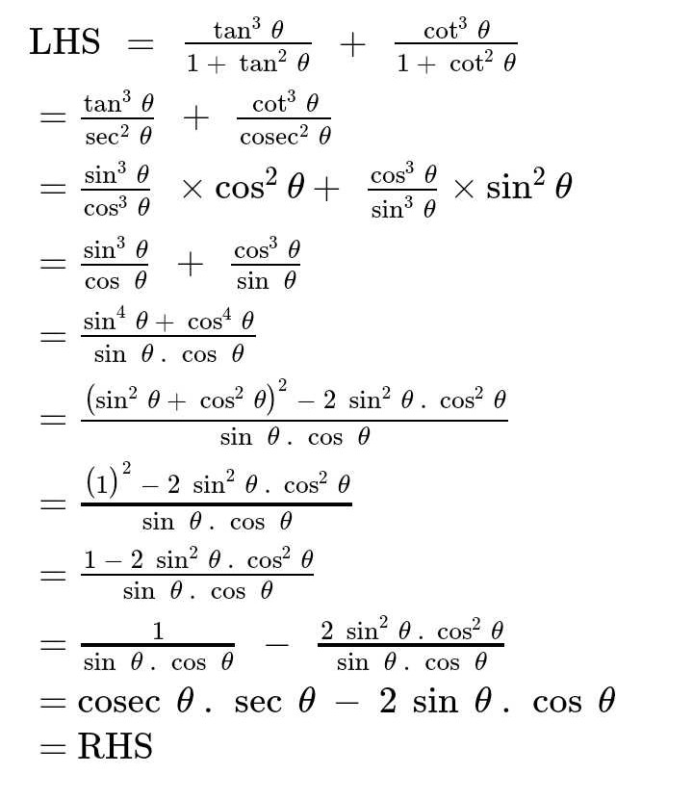


Prove If Tan 3 Theta 1 Tan 2 Theta Cot 3 Theta 1 Cot 2 Theta Sec Theta Cosec Theta 2 Sin Theta Cos Theta Edurev Class 10 Question
The Pythagorean Identity sin 2 θ cos 2 θ = 1 can be taken as sin 2 θ = 1 cos 2 θ and Equation (4) will become $\cos 2\theta = \cos^2 \theta (1 \cos^2 \theta)$ $\cos 2\theta = 2\cos^2 \theta 1$Join / Login maths General value of θ satisfying the equation tan 2 θ s e c 2 θ = 1 is _____?Using the formula tan 2A = 2 tan A/(1 – tan 2 A), (2 tan θ)/ (1 – tan 2 θ) tan θ = 1 2 tan 2 θ = 1


If Tan 2theta 1 2tan 2a Then Prove That 2sin 2theta 1 Sin 2a Mathematics Topperlearning Com 47



Solved Prove The Following Identities Tan 2theta 2 Tan Chegg Com



What Is The Formula For Tan 2 Theta


Solution Prove Sin 2theta 2tan Theta 1 Tan 2 Theta



Art Of Problem Solving



Understanding Pythagorean Identities Studypug



Prove That 1 Tan 28 1 Cot 28 1 Tan8 1 Cot8 2 Tan 28



Cos 2 Theta 1 Tan Theta Sin 3 Theta Sin Theta Cos Theta 1 Sin Theta Cos Theta Brainly In



5 1 5 2 Trigonometric Identities Ppt Download



1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube


If Tan Theta Cot Theta 2 Then What Is The Value Of Tan Squared Theta Cot Squared Theta Equal To Quora



त र क णम त य सर वसम क ओ क स च व क प ड य Trigonometric Functions Math Methods Math Formulas



Solved Prove The Given Identity Cos 2 Theta 1 Tan2 Th Chegg Com



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic
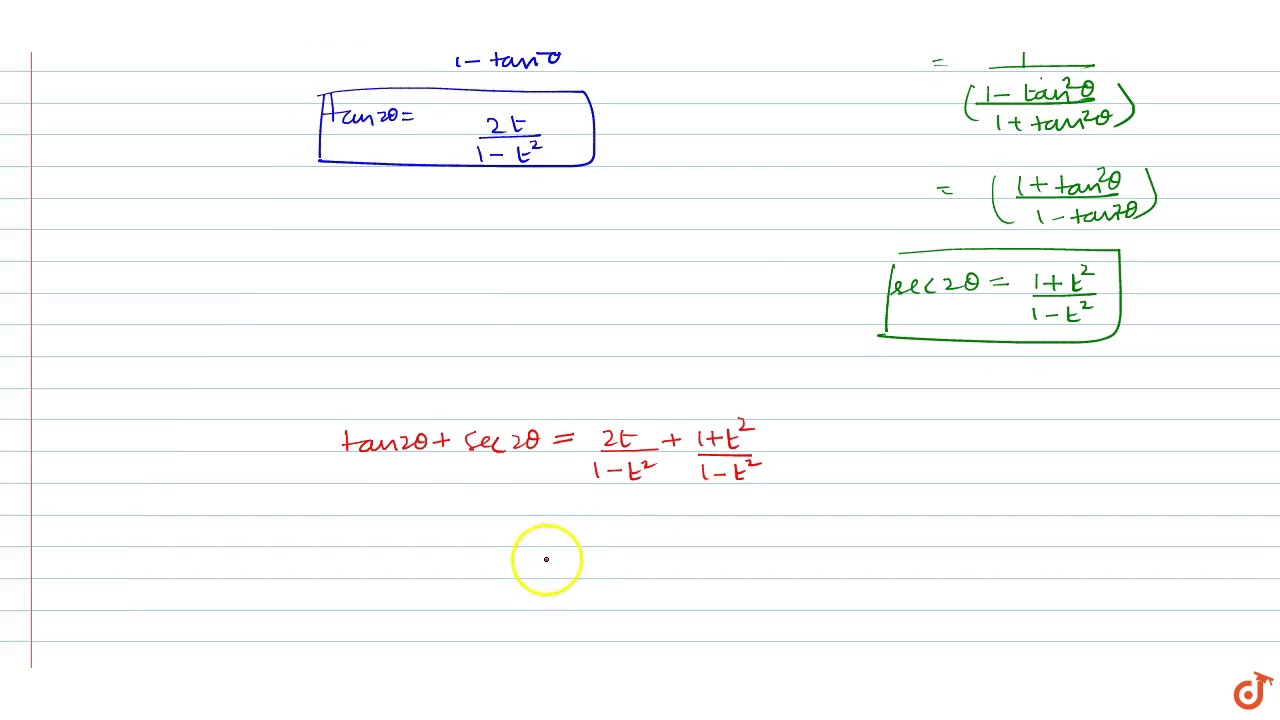


If Tan Theta T Then Tan 2 Theta Sec 2 Theta Youtube



Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions



Understanding Pythagorean Identities Studypug



5 1 Fundamental Trig Identities Reciprocal Identities Sin


What Is The Formula Of Tan2x Quora



Summary Of Trigonometric Identities


Derivatives Of Trigonometric Functions


How Do You Verify Tan 28 Sin 28 Tan 28sin 28 Socratic



Sin 2 Theta Is Equal To 2 Tan Theta Upon 1 Tan Square Theta And Theta 30 Degree Brainly In



Sec 2 Theta 1 Tan 2 Theta Youtube
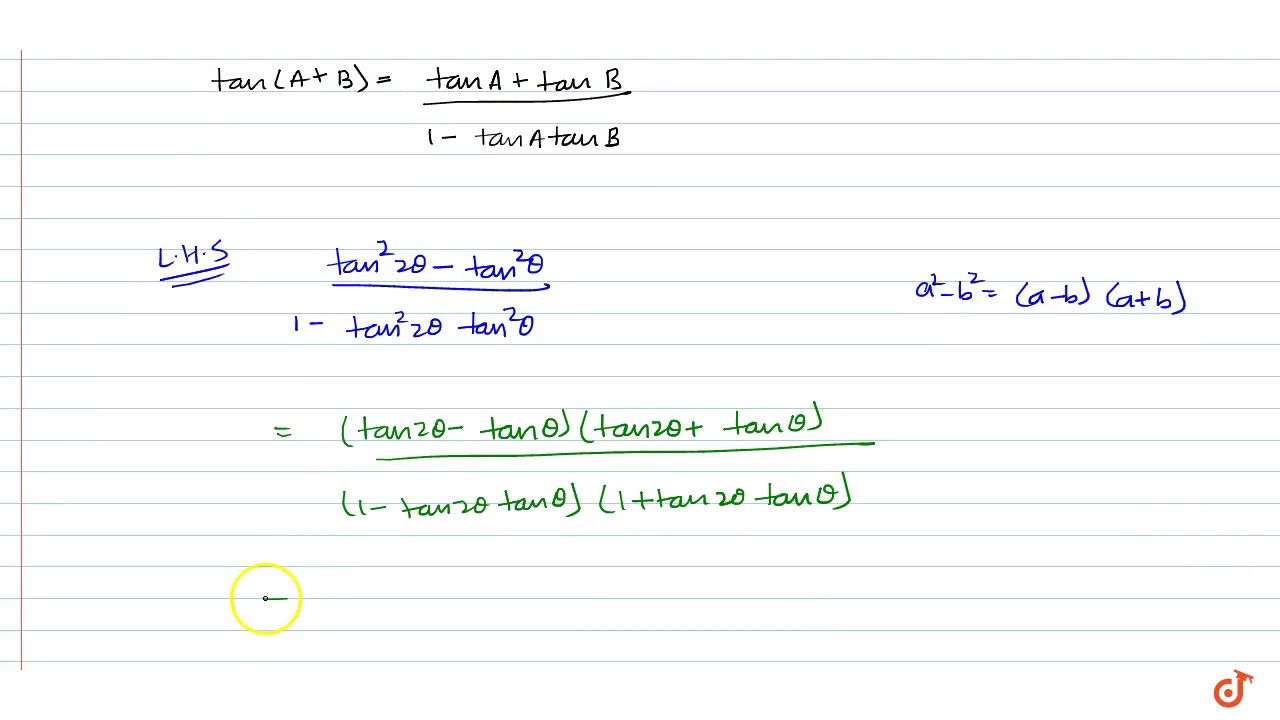


Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Theta Tan 3theta Tan Theta Youtube



Trigonometric Identities 1 Conditional Trigonometrical Identities We Have Certain Trigonometric Identiti Maths Solutions Math Methods Simplifying Expressions


How To Solve The Equation 2 Tan Theta Cot Theta 1 Quora



Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Th



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Prove Cos 2theta 1 Tan Theta Sin 3 Theta Sin Theta Cos Theta 1 Sin Theta Cos Brainly In


Tinkutara Equation Editor Math Forum Question



Proof Tan 2 1 Sec 2 Youtube
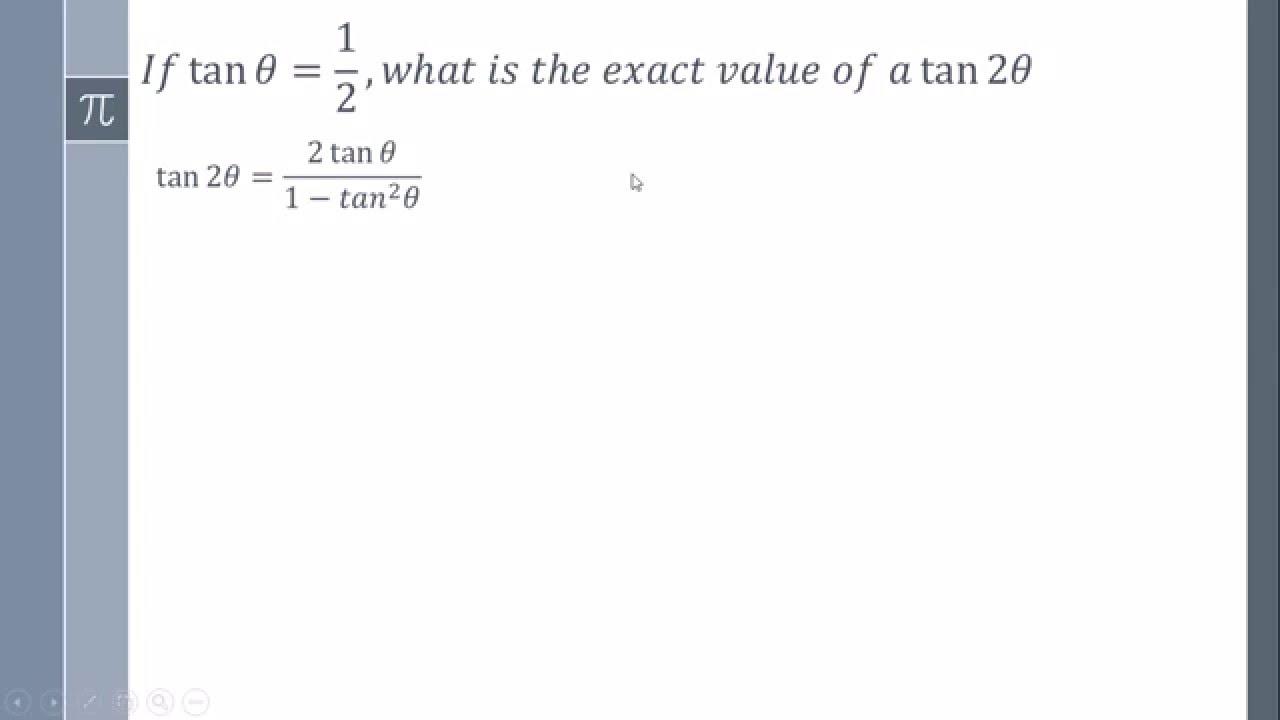


If Tan Of Theta Is 1 2 What Is The Exact Value Of Tan 2 Theta Youtube



Tangent Half Angle Formula Wikipedia



Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions



Tangent Half Angle Formula Wikipedia


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora
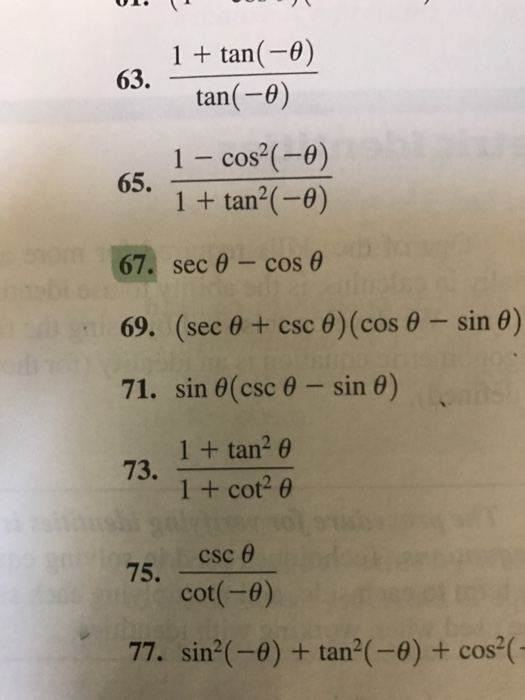


Solved 1 Tan Theta Tan Theta 1 Cos 2 Theta 1 Tan 2 Chegg Com



Ienvvsxb0bvtcm



Trigonometric Identities Topics In Trigonometry
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com


How I Remember Trig Identities Part 2 Beyond Solutions


18 Find The Cartesian Equation Of The Curve From The Parametric Equations X Tan 2 Theta And Y Sec Theta Where Pi 2 Theta Pi 2 Then Sketch It Width Indication Of
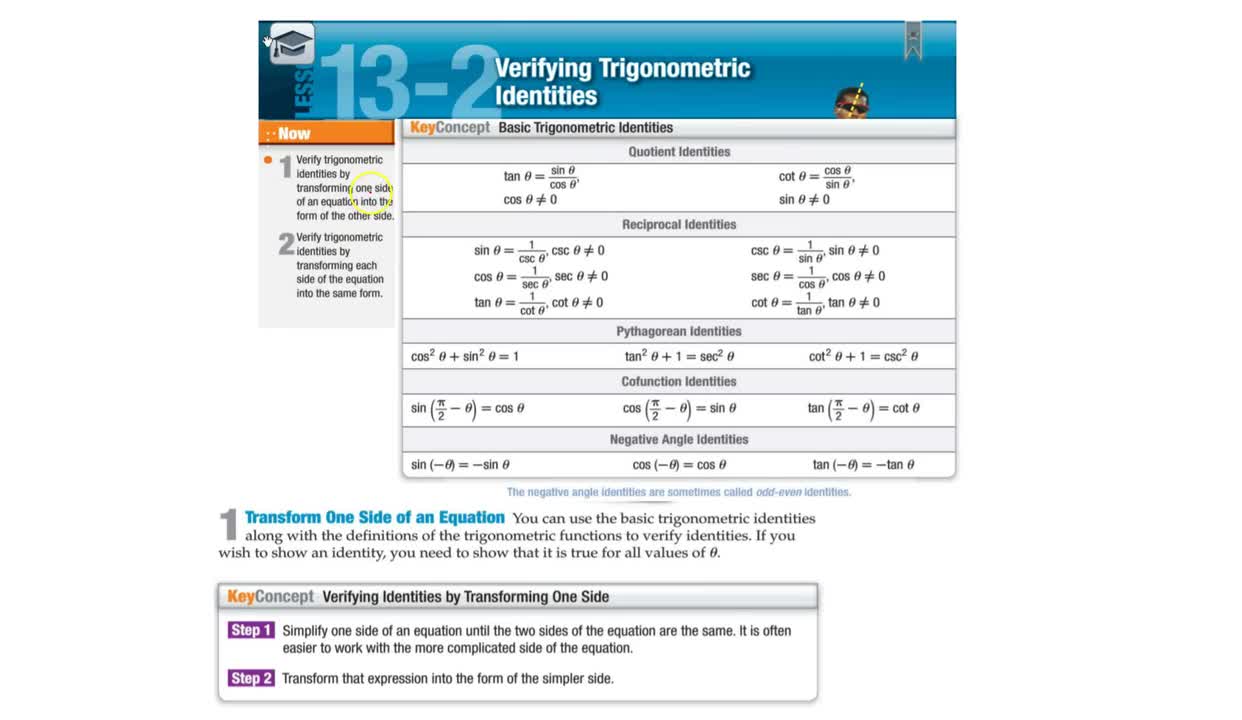


Honors Algebra 2 Trig Notes Chapter 13 Section 2 Bishop Amat Memorial High School



What Is The Value Of Sin 2theta 1 1 Tan 2theta


Solved 1 Tan2 Theta Sec2 Theta Verify That The Equati Chegg Com


Solving Trigonometric Equations With Identities Precalculus Ii
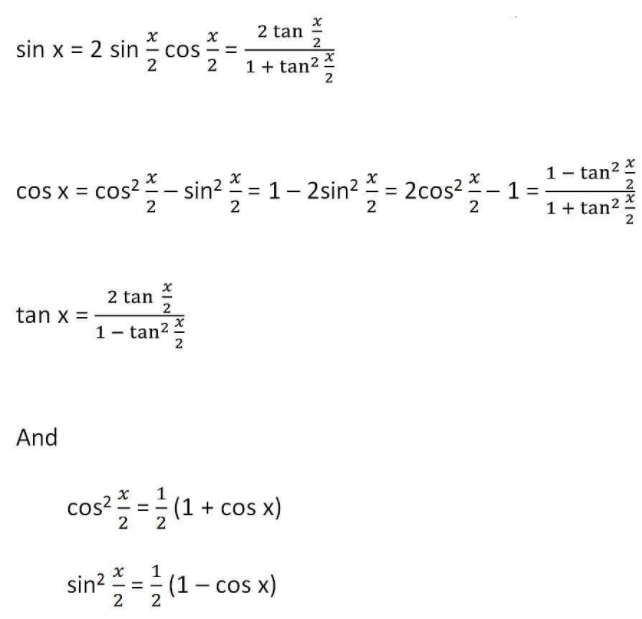


Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec



Trigonometric Identities List Of Trigonometric Identities Examples



Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com


Trigonometric Identities And Equations Ppt Download



Prove That Cot Theta 1 Tan Theta Cot Theta 2 Sec 2 Theta Maths Some Applications Of Trigonometry Meritnation Com



Example 9 Lines Where Tan 1 2 Where Is Inclination


5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download


Solution 1 Amp Tan Amp 2 Amp 952 1 Amp Cot Amp 2 Amp 952 1 Tan A 1 Cot A 2



30 The Number Of Roots Of The Equation 1 Tan Theta 1 Sin 2 Theta 1 Tan Theta For Theta In 0 2 Pi Is 2 C 5 0 4 D None Of These


Tangent Identities



5 1 Fundamental Trig Identities Reciprocal Identities Sin


Trigonometry Trigonometric Laws And Identities



Trigonometry Reciprocal Identities Expii
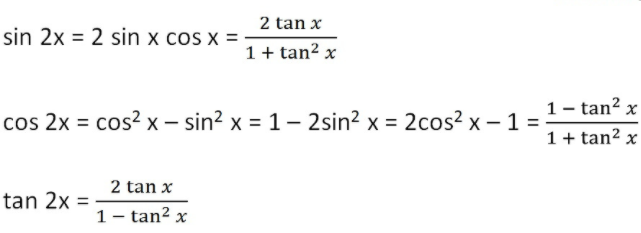


Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec



1 1 Tan 2 Theta 1 1 Cot 2 Theta 1 Sin 2 Theta Sin 4 Theta Brainly In



Tangent Half Angle Formula Wikipedia



Trigonometric Identities
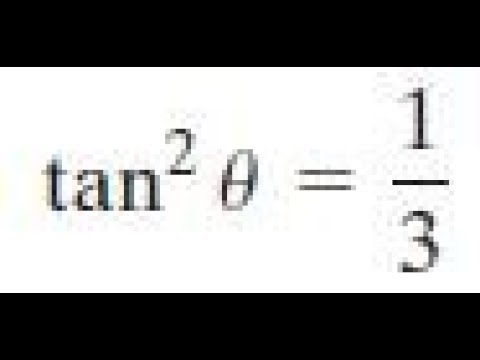


Tan 2 Theta 1 3 Solve For Interval 0 Less Theta Less 2pi Youtube



1 Tan 2theta 1 Cot 2theta 1 Tan Theta 1 Cot Theta 2 Tan 2 Theta Brainly In



If Tan 2 Theta 1 2 Tan 2 Phi Prove That Cos 2 Phi 1 2 Cos 2



Trigonometrical Ratios Or Functions A Plus Topper


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora
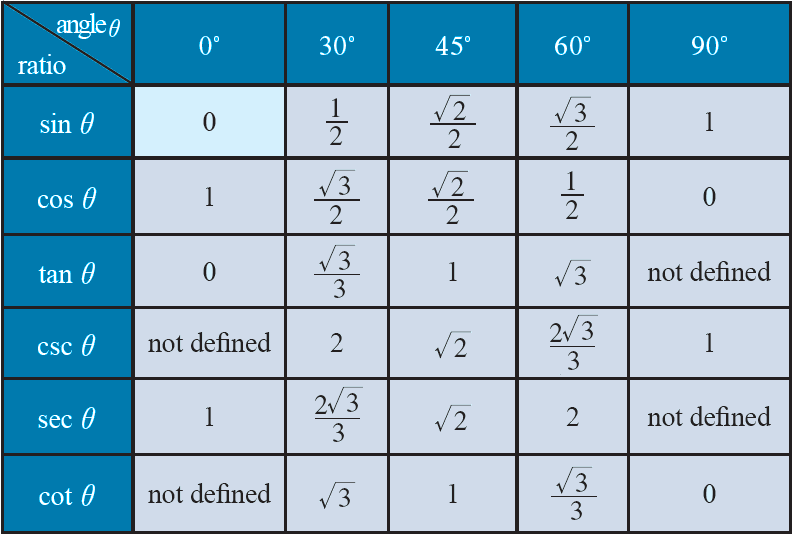


Trigonometric Identities


How Do You Prove 1 Sin 2theta 1 Cot 2theta Cot 2theta Socratic


Much From Little



Show 1 Tan 2theta 1 Sintheta 1 Sintheta 1



Solved Use The Trigonometric Identities To Simplify The E Chegg Com



Solve The Equation Tantheta Tan 2theta Tan 3theta 0



Prove That 1 Tan Theta Tan 2theta Sec 2theta Youtube



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Solving Sec Theta 1 Left Sqrt 2 1 Right Tan Theta Mathematics Stack Exchange



0 件のコメント:
コメントを投稿